字符串匹配

BF算法 / RK算法 / BM算法

BF（Brute Force）算法

Brute Force 的缩写，中文叫作暴力匹配算法，也叫朴素匹配算法。

作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，我们在主串中，检查起始位置分别是 0、1、2….n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的。

这种算法的最坏情况时间复杂度是 O(n*m)

RK（Rabin-Karp）算法

RK 算法的思路是这样的：我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等，那就说明对应的子串和模式串匹配了（这里先不考虑哈希冲突的问题）。因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了。

改进：
假设要匹配的字符串的字符集中只包含 K 个字符，我们可以用一个 K 进制数来表示一个子串，这个 K 进制数转化成十进制数，作为子串的哈希值。

比如：

十进制 567 = 510^2+610^1+7*10^0

26进制：abc = a26^2+b26^1+c26^0 = 026^2+126^1+226^0

a-b-c-d-e-f-g
a-b-c
b-c-d

得出这样的规律：相邻两个子串 s[i-1]和 s[i]（i 表示子串在主串中的起始位置，子串的长度都为 m），对应的哈希值计算公式有交集，也就是说，我们可以使用 s[i-1]的哈希值很快的计算出 s[i]的哈希值。如果用公式表示的话，就是下面这个样子：

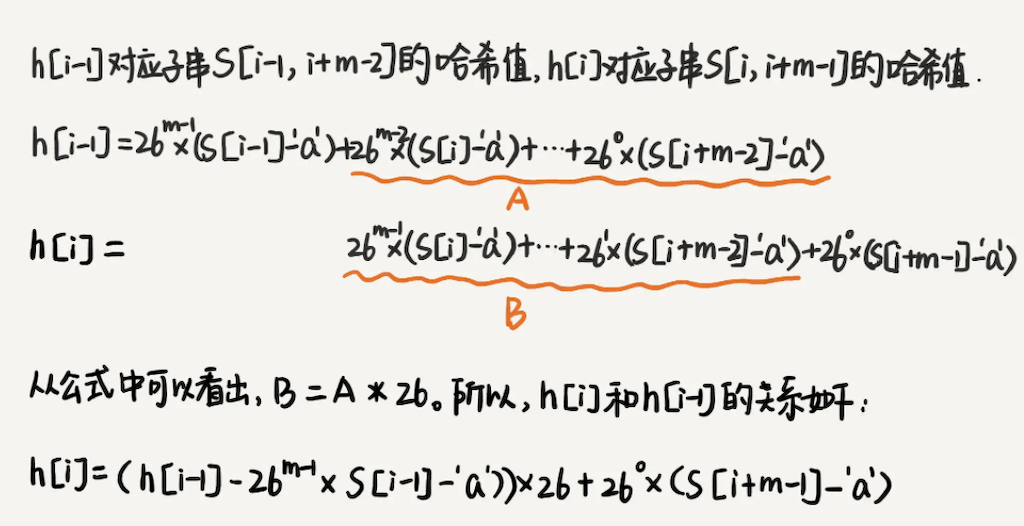
26^(m-1) 这部分的计算，我们可以通过查表的方法来提高效率。我们事先计算好 26^0、26^1、26^2……26^(m-1)，并且存储在一个长度为 m 的数组中，公式中的“次方”就对应数组的下标。当我们需要计算 26 的 x 次方的时候，就可以从数组的下标为 x 的位置取值，直接使用，省去了计算的时间。

整个 RK 算法包含两部分，计算子串哈希值和模式串哈希值与子串哈希值之间的比较。

  • 第一部分，只需要扫描一遍主串就能计算出所有子串的哈希值了，所以这部分的时间复杂度是 O(n)。

  • 第二部分，模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1)，总共需要比较 n-m+1 个子串的哈希值，所以，这部分的时间复杂度也是 O(n)。所以，RK 算法整体的时间复杂度就是 O(n)。

总结：

BF 算法是最简单、粗暴的字符串匹配算法，它的实现思路是，拿模式串与主串中是所有子串匹配，看是否有能匹配的子串。所以，时间复杂度也比较高，是 O(n*m)，n、m 表示主串和模式串的长度。不过，在实际的软件开发中，因为这种算法实现简单，对于处理小规模的字符串匹配很好用。

RK 算法是借助哈希算法对 BF 算法进行改造，即对每个子串分别求哈希值，然后拿子串的哈希值与模式串的哈希值比较，减少了比较的时间。所以，理想情况下，RK 算法的时间复杂度是 O(n)，跟 BF 算法相比，效率提高了很多。不过这样的效率取决于哈希算法的设计方法，如果存在冲突的情况下，时间复杂度可能会退化。极端情况下，哈希算法大量冲突，时间复杂度就退化为 O(n*m)。

BM （Boyer-Moore）算法

BM 算法包含两部分，分别是坏字符规则（bad character rule）和好后缀规则（good suffix shift）。

坏字符规则

从模式串的末尾往前倒着匹配，当发现某个字符没法匹配的时候，我们把这个没有匹配的字符叫
作坏字符（主串中的字符）。

我们拿坏字符 c 在模式串中查找，发现模式串中并不存在这个字符，也就是说，字符 c 与模式串中的任何字符都不可能匹配。这个时候，我们可以将模式串直接往后滑动，将模式串滑动到 c 后面的位置，再从模式串的末尾字符开始比较。

接下来，如果坏字符x在模式串中是存在的，模式串中下标是 0 的位置也是字符 x。这种情况下，我们可以将模式串往后滑动两位，让两个 x 上下对齐，然后再从模式串的末尾字符开始，重新匹配。

当发生不匹配的时候，我们把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在，我们把这个坏字符在模式串中的下标记作 xi。如果不存在，我们把 xi 记作 -1。那模式串往后移动的位数就等于 si-xi。（注意，我这里说的下标，都是字符在模式串的下标）。

如果坏字符在模式串里多处出现，那我们在计算 xi 的时候，选择最靠后的那个，因为这样不会让模式串滑动过多，导致本来可能匹配的情况被滑动略过。

利用坏字符规则，BM 算法在最好情况下的时间复杂度非常低，是 O(n/m)。比如，主串是 aaabaaabaaabaaab，模式串是 aaaa。每次比对，模式串都可以直接后移四位，所以，匹配具有类似特点的模式串和主串的时候，BM 算法非常高效。

不过，单纯使用坏字符规则还是不够的。因为根据 si-xi 计算出来的移动位数，有可能是负数，比如主串是 aaaaaaaaaaaaaaaa，模式串是 baaa。不但不会向后滑动模式串，还有可能倒退。所以，BM 算法还需要用到“好后缀规则”。

好后缀规则

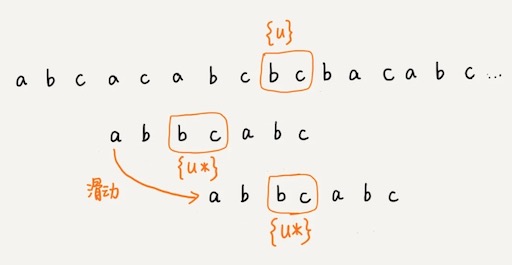
把已经匹配的 bc 叫作好后缀，记作{u}。我们拿它在模式串中查找，如果找到了另一个跟{u}相匹配的子串{u*}，那我们就将模式串滑动到子串{u*}与主串中{u}对齐的位置。

如果在模式串中找不到另一个等于{u}的子串，我们就直接将模式串，滑动到主串中{u}的后面，因为之前的任何一次往后滑动，都没有匹配主串中{u}的情况。

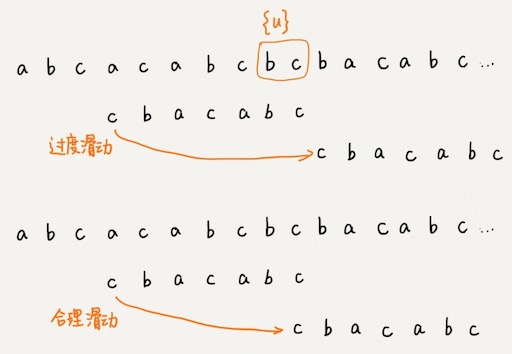
不过，当模式串中不存在等于{u}的子串时，我们直接将模式串滑动到主串{u}的后面。这样做有点太过头，所以，针对这种情况，我们不仅要看好后缀在模式串中，是否有另一个匹配的子串，我们还要考察好后缀的后缀子串，是否存在跟模式串的前缀子串匹配的。

我们可以分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最大的，作为模式串往后滑动的位数。这种处理方法还可以避免我们前面提到的，根据坏字符规则，计算得到的往后滑动的位数，有可能是负数的情况。

BM 算法代码实现

当遇到坏字符时，要计算往后移动的位数 si-xi，其中 xi 的计算是重点，我们如何求得 xi 呢？或者说，如何查找坏字符在模式串中出现的位置呢？

模式串中顺序遍历查找，这样就会比较低效

我们可以将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标了。

关于这个散列表，我们只实现一种最简单的情况，假设字符串的字符集不是很大，每个字符长度是 1 字节，我们用大小为 256 的数组，来记录每个字符在模式串中出现的位置。数组的下标对应字符的 ASCII 码值，数组中存储这个字符在模式串中出现的位置。

变量 b 是模式串，m 是模式串的长度，bc 表示刚刚讲的散列表。

这一步关键是为了提高查找模式串中坏字符位置的效率
如果模式串中前后有一样的字符，后面的会覆盖前面的位置

1
2
3
4
5
6
7
8
9
10
private static final int SIZE = 256; // 全局变量或成员变量
private void generateBC(char[] b, int m, int[] bc) {
  for (int i = 0; i < SIZE; ++i) {
    bc[i] = -1; // 初始化bc
  }
  for (int i = 0; i < m; ++i) {
    int ascii = (int)b[i]; // 计算b[i]的ASCII值
    bc[ascii] = i;
  }
}

这一步只使用了坏字符规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int bm(char[] a, int n, char[] b, int m) {
  int[] bc = new int[SIZE]; 
  generateBC(b, m, bc); // 构建模式串哈希表
  int i = 0; // i表示主串与模式串对齐的第一个字符
  while (i <= n - m) {
    int j;
    for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配
      if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j
    }
    if (j < 0) {
      return i; // 匹配成功，返回主串与模式串第一个匹配的字符的位置
    }
    // 这里等同于将模式串往后滑动j-bc[(int)a[i+j]]位
    i = i + (j - bc[(int)a[i+j]]); 
  }
  return -1;
}

这一步关键是为了提高查找模式串中，子串的匹配效率

引入最关键的变量 suffix 数组。suffix 数组的下标 k，表示后缀子串的长度，下标对应的数组值存储的是，在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值。

模式串：c a b c a b
0 1 2 3 4 5

后缀子串—长度—suffix(后缀位置)—prefix(前缀==后缀)
0000b 1 suffix[1]=2 0000c prefix[1] = false
000ab 2 suffix[2]=1 000ca prefix[2] = false
00cab 3 suffix[3]=0 00cab prefix[3] = true
0bcab 4 suffix[4]=-1 0cabc prefix[4] = false
abcab 5 suffix[5]=-1 cabca prefix[5] = false

不仅要在模式串中，查找跟好后缀匹配的另一个子串，还要在好后缀的后缀子串中，查找最长的能跟模式串前缀子串匹配的后缀子串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// b表示模式串，m表示长度，suffix，prefix数组事先申请好了
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
  for (int i = 0; i < m; ++i) { // 初始化
    suffix[i] = -1;
    prefix[i] = false;
  }
  for (int i = 0; i < m - 1; ++i) { // b[0, i]
    int j = i;
    int k = 0; // 公共后缀子串长度
    while (j >= 0 && b[j] == b[m-1-k]) { // 与b[0, m-1]求公共后缀子串
      --j;
      ++k;
      suffix[k] = j+1; //j+1表示公共后缀子串在b[0, i]中的起始下标
    }
    if (j == -1) prefix[k] = true; //如果公共后缀子串也是模式串的前缀子串
  }
}

假设好后缀的长度是 k。我们先拿好后缀，在 suffix 数组中查找其匹配的子串。如果 suffix[k]不等于 -1（-1 表示不存在匹配的子串），那我们就将模式串往后移动 j-suffix[k]+1 位（j 表示坏字符对应的模式串中的字符下标）。如果 suffix[k]等于 -1，表示模式串中不存在另一个跟好后缀匹配的子串片段。我们可以用下面这条规则来处理。

好后缀的后缀子串 b[r, m-1]（其中，r 取值从 j+2 到 m-1）的长度 k=m-r，如果 prefix[k]等于 true，表示长度为 k 的后缀子串，有可匹配的前缀子串，这样我们可以把模式串后移 r 位。

如果两条规则都没有找到可以匹配好后缀及其后缀子串的子串，我们就将整个模式串后移 m 位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// a,b表示主串和模式串；n，m表示主串和模式串的长度。
public int bm(char[] a, int n, char[] b, int m) {
  int[] bc = new int[SIZE]; 
  generateBC(b, m, bc); // 构建坏字符哈希表
  int[] suffix = new int[m];
  boolean[] prefix = new boolean[m];
  generateGS(b, m, suffix, prefix);
  int i = 0; // j表示主串与模式串匹配的第一个字符
  while (i <= n - m) {
    int j;
    for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配
      if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j
    }
    if (j < 0) {
      return i; // 匹配成功，返回主串与模式串第一个匹配的字符的位置
    }
    int x = j - bc[(int)a[i+j]];
    int y = 0;
    if (j < m-1) { // 如果有好后缀的话
      y = moveByGS(j, m, suffix, prefix);
    }
    i = i + Math.max(x, y);
  }
  return -1;
}

// j表示坏字符对应的模式串中的字符下标; m表示模式串长度
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
  int k = m - 1 - j; // 好后缀长度
  if (suffix[k] != -1) return j - suffix[k] +1;
  for (int r = j+2; r <= m-1; ++r) {
    if (prefix[m-r] == true) {
      return r;
    }
  }
  return m;
}
BM 算法核心思想是，利用模式串本身的特点，在模式串中某个字符与主串不能匹配的时候，将模式串往后多滑动几位，以此来减少不必要的字符比较，提高匹配的效率。BM 算法构建的规则有两类，坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存，为了节省内存，我们可以只用好后缀规则来实现 BM 算法。