图(Graph)一种非线性表数据结构,图中的元素我们就叫做顶点(vertex)。
图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫做边(edge)。
就拿微信举例子吧。我们可以把每个用户看作一个顶点。如果两个用户之间互加好友,那就在两者之间建立一条边。所以,整个微信的好友关系就可以用一张图来表示。其中,每个用户有多少个好友,对应到图中,就叫做顶点的度(degree),就是跟顶点相连接的边的条数。
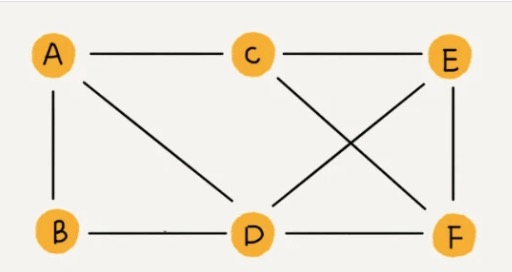
微博的社交关系跟微信还有点不一样,或者说更加复杂一点。如果用户 A 关注了用户 B,我们就在图中画一条从 A 到 B 的带箭头的边,来表示边的方向。如果用户 A 和用户 B 互相关注了,那我们就画一条从 A 指向 B 的边,再画一条从 B 指向 A 的边。我们把这种边有方向的图叫做“有向图”。以此类推,我们把边没有方向的图就叫做“无向图”。
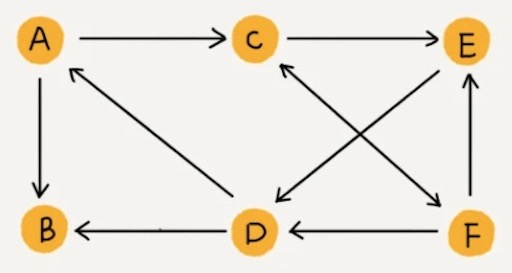
无向图中有“度”这个概念,表示一个顶点有多少条边。在有向图中,我们把度分为入度(In-degree)和出度(Out-degree)。
顶点的入度,表示有多少条边指向这个顶点;顶点的出度,表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子,入度就表示有多少粉丝,出度就表示关注了多少人。
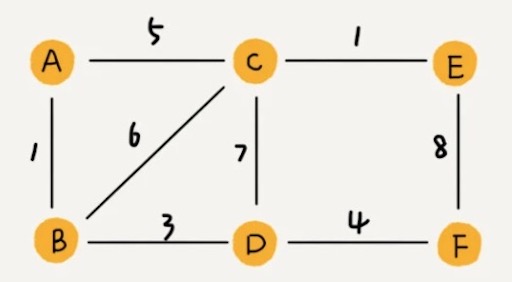
带权图(weighted graph),每条边都有一个权重(weight),我们可以通过这个权重来表示 QQ 好友间的亲密度。
邻接矩阵 存储方法
图最直观的一种存储方法就是,邻接矩阵(Adjacency Matrix)。
邻接矩阵的底层依赖一个二维数组。对于无向图来说,如果顶点 i 与顶点 j 之间有边,我们就将 A[i][j]和 A[j][i]标记为 1;对于有向图来说,如果顶点 i 到顶点 j 之间,有一条箭头从顶点 i 指向顶点 j 的边,那我们就将 A[i][j]标记为 1。同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i]标记为 1。对于带权图,数组中就存储相应的权重。
邻接矩阵的优点:简单,方便计算。缺点:浪费内存,特别是无向图和稀疏图。
邻接表存储方法
针对上面邻接矩阵比较浪费内存空间的问题,看另外一种图的存储方法,邻接表(Adjacency List)。
每个顶点对应的链表里面,存储的是指向的顶点。
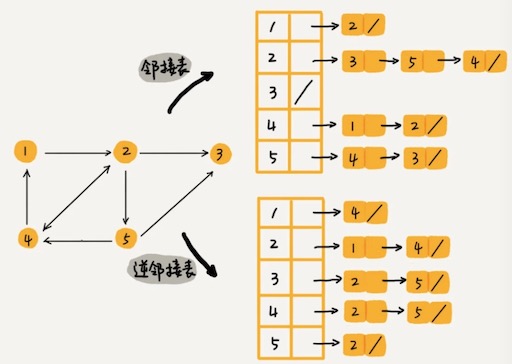
这个适合查看用户关注了哪些人,逆邻接表适合查看 某个用户被哪些用户关注了
链表的存储方式对缓存不友好。所以,比起邻接矩阵的存储方式,在邻接表中查询两个顶点之间的关系就没那么高效了。
微博这种有向图的解决思路,那像微信这种无向图,应该怎么存储呢?
可以使用邻接表的方式存储每个人所对应的好友列表。为了支持快速查找,好友列表可以使用红黑树存储。
符合图这种结构特点的例子还有很多,比如知识图谱(Knowledge Graph)。关于图这种数据结构,你还能想到其他生活或者工作中的例子吗?
- 互联网上网页之间通过超链接连接成一张有向图;
- 城市乃至全国交通网络是一张加权图;
- 人与人之间的人际关系够成一张图;
- Gradle这个编译工具,内部组织task的方式用的是有向图;
- CoordinatorLayout,其内部协调子view的联动,也是用的图;